Differenza tra interesse semplice e composto

Sai come funziona il calcolo degli interessi? E qual è la differenza tra l'interesse semplice e l'interesse composto? In questo articolo scopriremo in modo semplice e attraverso una serie di esempi numerici, in che modo il tuo denaro può acquisire un valore sempre maggiore anche grazie al tempo che scorre.

• Come si calcolano gli interessi?
• Calcolo interesse semplice
• Formula interesse semplice
• Esempi di calcolo interesse semplice
• Calcolo interesse composto
• Formula interesse composto
• Esempi di calcolo interesse composto
• Differenza tra interesse semplice e interesse composto: esempi a confronto

Iniziamo dal principio. Il tasso di interesse rappresenta la remunerazione del denaro investito, il rendimento che un determinato quantitativo di denaro ha per un certo periodo di tempo.
Dunque nel calcolo degli interessi, entrano in gioco tre elementi fondamentali:

• Il capitale;
• Il tasso di interesse, espresso in forma di percentuale;
• Il tempo.
  
  

Devi conoscere tasso di interesse e metodo di calcolo ogni volta che valuti un investimento o un finanziamento, cioè quando decidi di investire i tuoi risparmi oppure impegnarti finanziariamente per qualsiasi motivo.
Detto questo occorre sapere che il calcolo degli interessi cambia a seconda del regime di capitalizzazione degli interessi, che può essere:

• semplice;
• composto.

La differenza fra queste due metodologie di calcolo, come scopriremo, è fondamentale.

Per calcolare l'interesse semplice abbiamo bisogno dei tre elementi già citati: capitale totale, tasso di interesse e tempo durante il quale il capitale viene prestato. Andiamo nei dettagli e con qualche esempio:

• Capitale. Se parliamo di investimenti, il capitale totale su cui calcolare l'interesse semplice è l'intera somma che abbiamo deciso di investire.
• Tasso di interesse. La percentuale da applicare al capitale investito per determinarne la remunerazione. Ad esempio se hai investito in obbligazioni sarà la percentuale che ogni anno ti verrà corrisposta sulla somma che hai prestato all'emittente (Stato o impresa che sia).
• Tempo. Rappresenta la durata del prestito/investimento.

Con questi tre dati puoi calcolare, anche autonomamente, l'interesse semplice che andrai ad incassare in caso di investimento o a pagare in caso di finanziamento.

Prima di vedere la formula, ecco come possiamo rinominare gli elementi in gioco per esporla in maniere semplice:

• capitale (C);
• tasso di interesse (R);
• tempo (T).

Adesso siamo pronti per vedere la formula dell'interesse semplice:

C x R x T

Per semplificarti ulteriormente il calcolo, devi sapere che il tasso di interesse che viene normalmente riportato come una percentuale, può essere inserito nella formula in centesimi. Facciamo un esempio per chiarire: se il tasso è 3%, puoi inserirlo nella formula come 0,03 oppure se è pari al 4,5% puoi indicarlo come 0,045.

Veniamo ad un esempio numerico per comprendere il funzionamento della formula. Ecco i nostri dati:

• capitale 20.000 euro;
• tasso di interesse 2,5%, che come abbiamo visto possiamo esprimere come 0,025;
• tempo 1 anno.

Dunque abbiamo:
20.000 x 0,025 x 1 = 500

Proviamo adesso a variare l'importo del capitale. Ecco i nostri dati:

• capitale 10.000 euro;
• tasso di interesse 2,5%, che come abbiamo visto possiamo esprimere come 0,025;
• tempo 1 anno.

In questo caso il calcolo è il seguente:
10.000 x 0,025 x 1 = 250

Come puoi notare a capitale dimezzato, si dimezzano anche gli interessi. Questa è una caratteristica importante dell'interesse semplice, poiché è sempre proporzionale rispetto al capitale investito.

Veniamo all'ultimo esempio, variando il tempo:

• capitale 10.000 euro;
• tasso di interesse 2,5%, che come abbiamo visto possiamo esprimere come 0,025;
• tempo 3 anni.

Ecco il nostro calcolo:
10.000 x 0,025 x 3 = 750
Come puoi notare si tratta degli interessi calcolati per un anno e poi moltiplicati per 3, dunque sempre lo stesso importo (250 euro) moltiplicato per il numero di anni.

Ora che è chiaro il metodo di calcolo dell'interesse semplice, possiamo aggiungere un elemento di complessità. Ma niente paura, anche in questo caso andremo per gradi e vedremo degli esempi numerici.
La differenza fondamentale tra interesse semplice e interesse composto è che gli interessi maturati al termine di ogni periodo di capitalizzazione (che per semplicità considereremo pari ad un anno), vanno ad aggiungersi al capitale su cui vengono poi calcolati gli interessi per i periodi successivi.
Dunque ogni anno il capitale cresce e ogni anno gli interessi si calcolano su un capitale diverso e maggiore di quello dell'anno precedente.

Torniamo ai nostri simboli per illustrare la formula per il calcolo dell'interesse composto:

• capitale (C);
• tasso di interesse (r);
• tempo (t);
• montante (M).

La novità è la "M", cioè il montante: il valore del capitale rivalutato alla luce degli interessi maturati.
Ecco la nostra formula:

M = C x (1 + r)^t

Non avremo interessi proporzionali al capitale investito: questi infatti mostreranno una crescita esponenziale, poiché il tempo non è un moltiplicatore, ma appunto un valore esponenziale nella nostra formula.
Facciamo degli esempi per chiarire meglio il calcolo.

Partiamo dal periodo 1, che come vedremo con gli identici valori di partenza che abbiamo usato per l'interesse semplice, daranno il medesimo risultato. Ecco i dati:

• capitale 20.000 euro;
• tasso di interesse 2,5%, che come abbiamo visto possiamo esprimere come 0,025;
• tempo 1 anno.

Dunque abbiamo:
20.000 x (1+0,025)^1 = 20.500
I nostri interessi sono pari a 500 euro, esattamente come per l'interesse semplice.

E se i periodi fossero 2?
Ecco come cambia il nostro calcolo:
20.000 x (1+0,025)^2 = 21.012,50
Con l'interesse semplice avremmo ottenuto un montante pari a 21.000 (i 20.000 di partenza e poi 500 per ciascun anno), mentre in questo caso il montante è cresciuto di 12,50 euro in più.
Scomponiamo il calcolo per mostrarlo meglio, prendendo per il secondo anno i 20.500 euro come capitale (C) e calcolando il nuovo montante per un solo anno:
20.500 x (1+0,025)^1 = 21.012,50
Come avrai notato, la formula con la "t" messa all'esponente, ci serve semplicemente per evitare di calcolare gli interessi anno per anno e applicare la formula ogni volta fino alla fine del periodo.

Vediamo infine che cosa accade se i periodi fossero 3:
20.000 x (1+0,025)^3 = 21.537,81

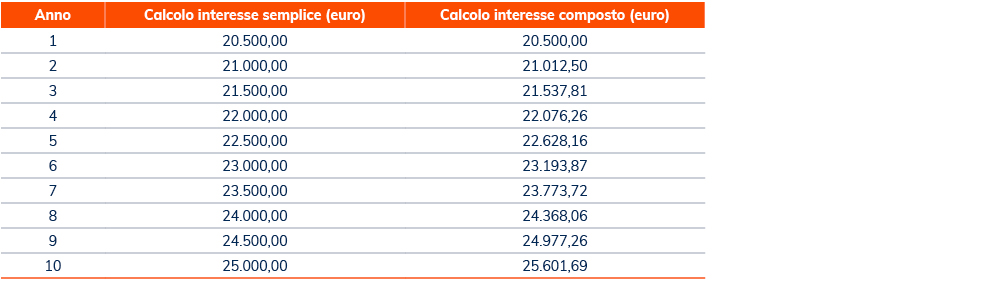
Se poi il tuo orizzonte temporale è molto lungo, ad esempio in caso di previdenza complementare, gli effetti dell'interesse composto sono ancora più interessanti. Se torniamo al nostro esempio, prendendo in considerazione 30 anni, i risultati sul montante saranno i seguenti:

• con il calcolo dell'interesse semplice 35.000,00 euro;
• con il calcolo dell'interesse composto 41.951,35 euro.